Introduction
Reinforcement Learning is part of a decades-long trend within artificial intelligence and machine learning toward greater integration with statistics, optimization, and other mathematical subjects. For example, the ability of some reinforcement learning methods to learn with parameterized approximators addresses the classical “curse of dimensionality” in operations research and control theory. More distinctively, reinforcement learning has also interacted strongly with psychology and neuroscience, with substantial benefits going both ways. Of all the forms of machine learning, reinforcement learning is the closest to the kind of learning that humans and other animals do, and many of the core algorithms of reinforcement learning were originally inspired by biological learning systems.
Trial-Error
According to Richard S. Sutton and Andrew G. Barto [1]–the first authors to use the term–Reinforced Learning Reinforcement learning is about what to do, that is, how to map situations to action so that we optimize a reward. The learner must discover which action yield the best reward by trying them. In the most general sense, action may not only affect immediate reward but also the next situation and, through that, all subsequent rewards.
Sensation action and goal
At the same time, Reinforcement Learning encloses a problem, a class of solution methods, and the field that studies this problem and its solutions. Its formalism is based on the theory of controlled dynamical systems, with a strong focus on the optimal control of partially known Markov decision processes. Then, the core idea consists of capturing the essence of the problem when an agent learns through experience and interaction to reach a goal. This agent can sense the state of its environment to some extent and must be able to take action that affects the state. The agent also must have a goal or goals related to the state of the environment.
MDPs are designed to incorporate three essential elements: sensation, action, and goal. Therefore, any approach suitable for solving such problems should be considered a potential method for Reinforcement Learning.
Refrences
Exploration-exploration dilemma and uncertainty
To obtain the best reward, the agent must prefer actions used in the past and perceived as effective to produce a reward. However, to discover such actions, the agent must try actions never used before. So, there is a delicate trade-off between exploiting and exploring. The agent has to exploit its knowledge to produce a reward but simultaneously has to explore to improve its reward in the future. Here, our dilemma is that neither exploration nor exploitation can be pursued exclusively without failing the task.
Another essential aspect of reinforcement learning is that it specifically deals with the entire process of a goal-directed agent interacting with an uncertain environment. This aspect differs from many approaches that only focus on subproblems rather than considering how they might contribute to the bigger picture. For example, many machine learning researchers have studied supervised Learning without specifying how such an ability would ultimately be helpful. Other researchers have developed planning theories with general goals without considering planning’s role in real-time decision-making or whether the predictive models necessary for planning are well suited. Although these approaches have produced valuable results, their focus on isolated subproblems leads to significant limitations.
Reinforcement learning takes the opposite approach, beginning with a fully interactive, goal-seeking agent. In reinforcement learning, the agent has explicit goals, can sense aspects of their environment, and can choose actions to influence its environment.
Examples
A master chess player makes a move.
An adaptive controller adjusts parameters of a petroleum refinery’s operation in real time.
A gazelle calf struggles to its feet minutes after being born.
A mobile robot decides whether it should enter a new room in search of more trash to collect or start trying to find its way back to its battery recharging station.
Phil prepares his breakfast
The (possible) 4 elements of Reinforcement Learning
Given an agent, we identify four main element in a reinforcement learning model:
a policy, a reward, a value function and (optionally) a model of the environment.
- Policy
-
A policy is as a set of actions that guide the agent to respond according to its perception of the environment. It’s like a set of instructions that tell the agent what to do when it encounters a certain situation. In general, policies may be stochastic, specifying probabilities for each action.
- Reward
-
The reward signal thus defines what are the good and bad events for the agent. In a biological system, we might think of rewards as analogous to the experiences of pleasure or pain. They are the immediate and defining features of the problem faced by the agent. The reward signal is the primary basis for altering the policy; if an action selected by the policy is followed by low reward, then the policy may be changed to select some other action in that situation in the future. In general, reward signals may be stochastic functions of the state of the environment and the actions taken.
- Value function
-
Whereas the reward signal indicates what is good in the immediate sense, a value function specifies what is good in the long run. In simple terms, the value of a state represents the total reward an agent can anticipate to receive in the future, beginning from that state. While rewards reflect the immediate appeal of environmental states, values signify the long-term appeal of states, considering the potential future states and the rewards they offer. For example, a state might consistently yield a low immediate reward but still have a high value because it is regularly followed by other states that yield high rewards. Alternatively, the opposite could also be true. Rewards can be compared to pleasure (when high) and pain (when low). At the same time, values represent a more precise and long-term assessment of how satisfied or dissatisfied we are with the state of our environment. In a sense, rewards are primary, whereas values, as predictions of rewards, are secondary. Without rewards, there could be no values, and the only purpose of estimating values is to achieve more rewards. Action choices are made based on value judgments. We seek actions that bring about states of highest value, not highest reward, because these actions obtain the greatest amount of reward for us over the long run. In fact, the most important component of almost all reinforcement learning algorithms we consider is a method for efficiently estimating values.
- Environment model
-
The environment model is something that mimics the behavior of the environment or, more generally, that allows inferences to be made about how the environment will behave. For example, given a state and action, the model might predict the resultant next state and next reward. Models are used for planning. This means making decisions by considering potential future situations before they occur. For our purposes, the environment can be represented as a dynamic system through an ordinary differential equation or a discrete finite difference equation.
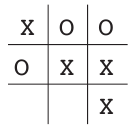
A toy RL-exmaple: Tic-Tac-Toe
To illustrate the general idea of reinforcement learning and contrast it with other ap- proaches, we next consider a single example in more detail.
Consider the familiar child’s game of tic-tac-toe.
Although the tic-tac-toe game is a simple problem, it cannot be satisfactorily solved using classical techniques.
For instance, the classical “minimax” solution from game theory is not applicable here because it assumes the opponent’s specific way of playing. A minimax player would never reach a game state from which it could lose. Even if, in reality, it always won from that state due to incorrect play by the opponent. The classical optimization methods for sequential decision problems, like dynamic programming, can find the best solution for any opponent. However, these methods need a detailed description of the opponent as input, including the probabilities of the opponent’s moves in each board state.
Alternatively, this information can be estimated through experience, such as playing numerous games against the opponent. The best approach to this problem is to first learn a model of the opponent’s behavior with a certain level of confidence, and then use dynamic programming to calculate an optimal solution based on the approximate opponent model.
Sutton and Barto [see pp. 9-12 1] propose the following way to approach tic tac toe with Reinforcement Learning:
Refrences
Setup:
First we would set up a table of numbers (or labels), one for each possible state of the game.
Each number will be the latest estimate of the probability of our winning from that state.
We treat this estimate as the state’s value, and the whole table is the learned value function.
State \(A\) has higher value than state \(B\), or is considered ‘better’ than state \(B\), if the current estimate of the probability of our winning from \(A\) is higher than it is from \(B\).
If we always play \(Xs\), then for all states with three \(Xs\) in a row the probability of winning is 1, because we have already won.
Similarly, for all states with three \(Os\) in a row, or that are filled up, the correct probability is 0–we cannot win from them.
We set the initial values of all the other states to \(0.5\), representing a guess that we have a 50% chance of winning.
Training:
We then play many games against the opponent.
To select our moves we examine the states that would result from each of our possible moves (one for each blank space on the board) and look up their current values in the table. Most of the time we move greedily,selecting the move that leads to the state with greatest value, that is, with the highest estimated probability of winning.
Occasionally, however, we select randomly from among the other moves instead. These are called exploratory moves because they cause us to experience states that we might otherwise never see.
A sequence of moves made and considered during a game can be diagrammed as the following figure: